数据结构笔记

算法的时间复杂度

假如fn是一个多项式，忽略所有低次幂以及最高次幂的系数

O(1)

线性阶

二叉树

二叉树的应用：主要是数据存储，例如 Windows/Linux 文件系统；便于搜索和排序。

部分关键词：

• 深度：有几层
• 节点：有几个点
• 度：一个节点有几个分支

类型：

• 满二叉树：是完全二叉树，
• 完全二叉树：节点 自上而下从左到右 不存在间隔

二叉树的存储结构：

1. 顺序存储结构
2. 链式存储结构

1.顺序存储结构

首先看一下完全二叉树的顺序存储，一颗完全二叉树如图1-1所示。

将这颗二叉树存入到数组中，相应的下标对应其同样的位置，如图1-2所示。

可以看出完全二叉树的优越性。由于它定义的严格，所以用顺序结构也可以表现出二叉树的结构来。
当然对于一般的二叉树，尽管层序编号不能反映逻辑关系，但是可以将其按完全二叉树编号，只不过，把存在的结点设置为“^”而已。如图1-3中，注意浅色结点表示不存在。

考虑一种极端的情况，一颗深度为k的右斜树，他只有k个结点，却需要分配2 k-1个存储单元，这显然是对存储空间的浪费，例如图1-5所示，所以顺序存储结构一般只用于完全二叉树。

原文链接：https://blog.csdn.net/xiangjunyes/article/details/106871111

2.链式存储结构

二叉链表
既然顺序存储的适用性不强，我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子，所以为他设计一个数据域和两个指针域是比较自然的想法，我们称这样的链表叫做二叉链表，结构如图1-6所示。

其中data是数据域，lchild和rchild是是指针域，分别存放指向左孩子和右孩子的指针。

1
2
3
4
5
6

//二叉树的二叉链表结点结构定义
typedef struct BiNode
{
	TElemType data;    				//结点数据
	struct BiTNode *lchild,*rchild;  //左右孩子指针
}

结构示意图如图1-7所示。

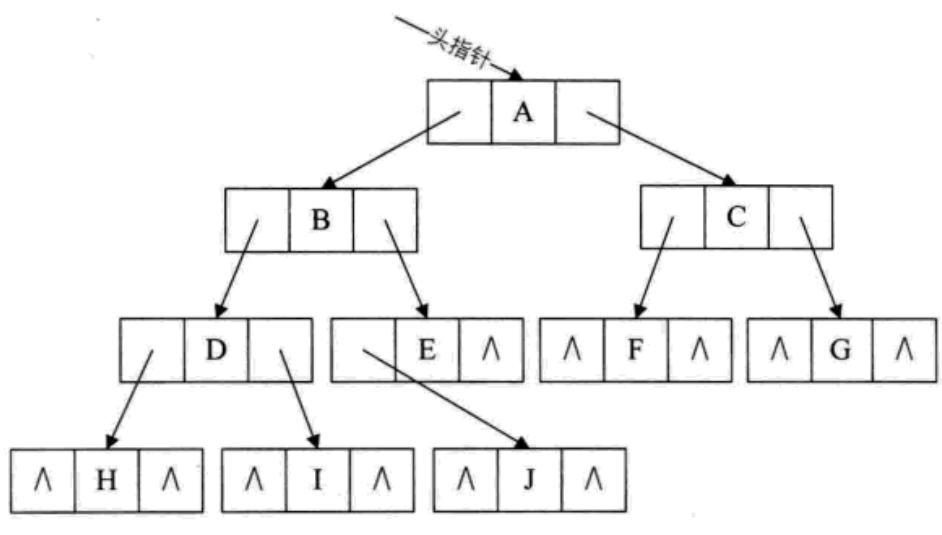
原文链接：https://blog.csdn.net/xiangjunyes/article/details/106871111

先根，中根，后根

1. 先根遍历
   结果：ABCDEFGH
   原理：先遍历根节点，再遍历左子树，最后遍历右子树；
2. 中根遍历
   结果：CBEDFAGH
   原理：先遍历左子树，再遍历根节点，最后遍历右子树；
3. 后根遍历
   结果：CEFDBHGA
   原理：遍历左子树，再遍历右子树，最后遍历根节点；

图解二叉树先根、中根、后根遍历

线性表

栈和队列

串、数组、广义表

树和二叉树

广度优先遍历：从左到右，从上到下

深度优先遍历：从上到下，从左到右